Code of the Week #8: solver PCG

OpenFOAM
1

前面已经基本了解了 OpenFOAM 对方程是如何离散的，即对 PDEs (偏微分方程, Partial Differential Equations) 离散成矩阵的乘法，以方便计算机求解：

\mathbf{A}\varphi=\mathbf{Q} \tag{1}

式中， \mathbf{A} 为矩阵的系数， \varphi 为待求的未知数向量， \mathbf{Q} 为已知向量。

计算机在求解这些方程时，针对方程的特点，也提供了很多的选择，如何选择方程求解的算法，OpenFOAM 将会读取一个设置文件，即位于算例文件夹下的 system/fvSolution 文件，该文件 的一部分如下：

solvers                       // 求解矩阵的算法设置
{
    p                         // 求解变量 p
    {
        solver          PCG;  // 求解的方法，preconditioned conjugate gradient
        preconditioner  DIC;  // 预处理方法，
        tolerance       1e-06;// 绝对误差
        relTol          0.1;  // 相对误差
    }
}
...

即：对于 p 变量 (场)，采用预处理共轭梯度法 (Preconditioned Conjugate Gradient)，预处理方法为 DIC (Diagonal-based Incomplete Cholesky)，收敛的条件是，绝对误差小于 1e-6，相对误差小于 0.1。

线性方程组的解法有：直接法、迭代法。直接法有：高斯消去法、分解法。迭代法有：经典的 (Jacobi，Gauss-Siedel，SOR，SSOR)，现代的 (FOM, IOM, DIOM, CG, PCG, GMRES, GCR, BiCG, CGS, …)。方法有很多，到底怎么选择？甚至 :sweat: 这些缩写是什么鬼？

任何方程组都可以使用直接法求解；直接法求解某些方程组特别耗时；但是离散格式的误差要比计算机的计算误差要大得多，因此，也没有必要获得精确解，只要计算结果的准确度比离散格式更小就可以了。

首先，N-S 方程离散后形成的某一未知数的方程组的未知数的数量就是网格的数量，一般都是以千计，复杂的网格或精细的网格动则百万、千万，如果要计算某一城市区域的风场，可能会有上亿的网格，一般情况下都会采用迭代法来计算。

:mega: 前方高能预警，理论性较强，但每一个学过矩阵的同学都应该能看明白。

考虑如式 (1) 的矩阵方程，于 n 次迭代后，获得一并不满足方程的近似解 \varphi^n ，则矩阵方程的残差 \rho^n 为

\mathbf{A} \varphi^n = \mathbf{Q}-\rho^n \tag{2}

(1)-(2) 可得

\mathbf{A} \epsilon^n=\mathbf{A}(\varphi - \varphi^n) = \rho^n \tag{3}

迭代的目的就是要使 \rho 趋近于 0，在这一过程中， \epsilon 也趋近于 0 。考虑一个线性方程组，以下面的格式

M\varphi^{n+1} = N\varphi^n + B \tag{4}

当收敛时， \varphi^{n+1} = N\varphi^n=\varphi ，则

A=M-N,\quad\text{and}\quad B=Q

更一般的情况是

PA=M-N,\quad\text{and}\quad B=PQ

式中， P 为非奇异预处理矩阵。

当收敛时，有

M\varphi = N\varphi + B \tag{5}

(4)-(5) 有

M\epsilon^{n+1} = N\epsilon^n

即

\epsilon^{n+1} = M^{-1} N\epsilon^n \tag{6}

如果 \lim_{n\to \infty}\epsilon^n=0 ，则认为迭代收敛。

关键的部分是矩阵 M^{-1} N 的特征值 \lambda_k 和特征向量 \psi^k ：

M^{-1} N=\lambda_k \psi^k,\quad k = 1,\,2,\,...,K,

K 是方程的数目 (网格的数目)。

假设特征向量形成一完备的向量空间，包含了所有的 n- 向量。则初始偏差

\epsilon^0 = \sum_{k=1}^K a_k\psi^k

式中， a_k 为一常数。则下一步迭代的误差为

\epsilon^1 = M^{-1} N \epsilon^0= M^{-1} N\sum_{k=1}^K a_k\psi^k=\sum_{k=1}^K a_k \lambda_k \psi^k

以此类推，有

\epsilon^n = \sum_{k=1}^K a_k (\lambda_k)^n \psi^k

从上式可以看出， \epsilon^n\to 0 充要条件是所有的 |\lambda_k| < 1 。最大的 \lambda_k 称为 M^{-1} N 的谱半径。当迭代一定次数后，包含较小的特征值的项会变得更小，而仅有最大的特征值项得以保留下来：

\epsilon^n \approx a_1(\lambda_1)^n\psi^1

我们定义收敛为迭代误差小于一定量 \delta ，则

\approx a_1(\lambda_1)^n\approx \delta

两边取对数，有

n\approx\frac{\ln(\delta/a_1)}{\ln \lambda_1}

可以看出，若 \lambda_1 相当接近于 1，则收敛会很慢。

以线性方程为例，

ax=b

使用迭代的方法，注意 m=a+n ，且 p 迭代步数：

mx^{p+1} = nx^p + b

则其误差服从式 (6)

\epsilon^{p+1} = \frac{n}{m}\epsilon^p

可以看出，当 n/m 很小时，误差减小得很快，也可以说当 n 很小时， m\approx a 。当解线性方程组时，类似的结论为： M 与 A 越接近，收敛得越快。

:sleepy: 睡着了没？

因此，重要的问题是如何找到合适的 M 和 N ，假设使用 LU 分解，有

M=LU=A+N

如果 A 是对称矩阵，这一分解方式就是 Incomplete Cholesky 分解法，常用于共轭梯度法。OpenFOAM 则使用这一方法的 diagonal 版本，称为 Simplified Diagonal-based Incomplete Cholesky preconditioner (DIC)。对流－扩散或 N-S 方程离散得到的矩阵是非对称矩阵，因而不能使用这一方法，其对应的为 Incomplete LU (ILU) 分解。

:thinking: 到这里了，还没完？？？

PCG 就是预处理共轭梯度法 (Preconditioned Conjugate Gradient method)，在讲 CG 之前，还得提到最速下降法 (Steepest Descent)。在这之前，还有一些要说的，不急哈。

说一个矩阵 A 是正定的，就是说它与一个非零向量 x 的关系是

x^T A x >0

不明就里。那先忽略吧。

一个向量的二次型是一个标量，

f(x)=\frac{1}{2} x^T A x - b^T x +c

长话短说，当 A 对称且正定的， x 的解使 f(x) 最小。

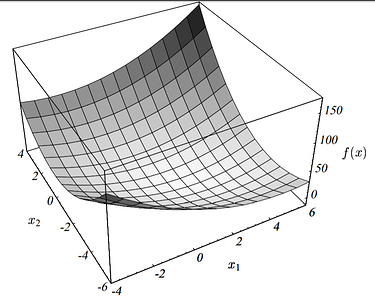
例： 有这样一个方程，

A=\left[ \begin{array}% 3 & 2 \\ 2& 6 \\ \end{array} \right],\, b=\left[ \begin{array}% 2 \\ -8 \\ \end{array} \right],\, c=0

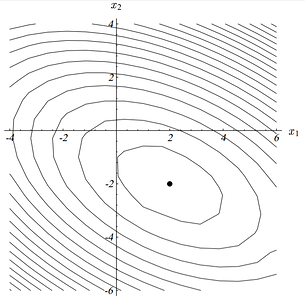
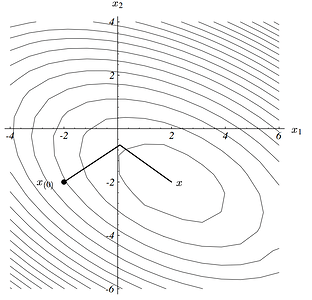
其方程组可以画出如下的图，这个图的最小点就是方程的解。

quadratic-form-plot
quadratic-form-plot861×689 117 KB

这个图的等值线图为
quadratic-form-contour
quadratic-form-contour623×613 92.7 KB

梯度 (场) f'(x) 为
quadratic-form-contour-grad
quadratic-form-contour-grad628×613 85.2 KB

经过一阵推导，

f'(x) = \frac{1}{2} A^T x + \frac{1}{2} A x - b

由于 A 是对称的 (A^T = A)，因此，

f'(x) =A x - b

设 f'(x) = 0 ，我们就还原了方程 Ax=b 。则方程的解 x 是 f(x) 的极值点。当 A 对称且正定，方程的解使 f(x) 最小。当 A 不对称时，求 \dfrac{1}{2}(A^T + A) x =b 。

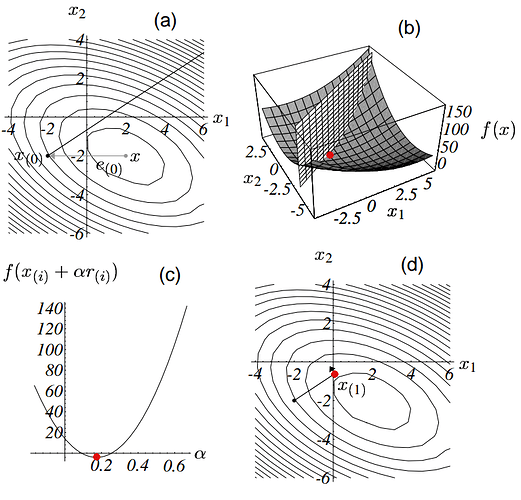
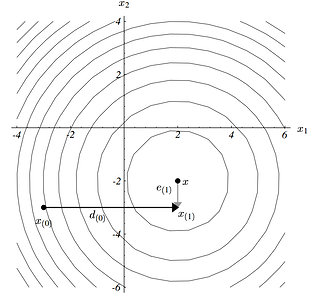
最速下降法就是：以任意点 x_{(0)} 为起点，经过一系列步骤 x_{(1)} , x_{(2)}, …, 最终达到与方程的解 x 足够近。

quadratic-form-contour-steepest
quadratic-form-contour-steepest771×760 105 KB

每一次搜寻都使 f(x) 在其梯度方向最小，
quadratic-form-contour-lineSearch
quadratic-form-contour-lineSearch768×737 163 KB

接着从这个点开始重复上面的方法，最终可获得方程的解。

但是，最速下降法的效率并不高。怎样才能最少步数求解？假设使用正交的坐标方向，两步就搞定。

quadratic-form-contour-conjugateDirection
quadratic-form-contour-conjugateDirection795×753 85 KB

问题来了，我们并不知道 x 是多少。稍作变换
quadratic-form-contour-conjugateD
quadratic-form-contour-conjugateD589×563 77.2 KB

不一定使用坐标的，方案是使搜寻的方向 A-正交，两个向量 d_{(i)},\, d_{(j)} 如果满足条件

d_{(i)}^T A d_{(j)} =0

称为 A-正交或共轭。这个方法叫共轭方向法。那么，怎么创建共轭方向？

CG 就是创建残量的共轭为搜寻方向的共轭方向法。

quadratic-form-contour-CG
quadratic-form-contour-CG780×750 104 KB

来自 wiki 的步骤：
cg-algo

:relieved:好像明白点了。那 PCG 又是什么？为什么要做 pre-conditioning. 因为，矩阵的条件数越大，收敛越慢。如果能将原始方程转换为等价的、条件数 (condition number) 较小的方程，可以使收敛速度加快。啥是条件数？ 条件数表示矩阵计算对于误差的敏感性。对于线性方程组 $Ax=b$，如果 A 的条件数大， b 的微小改变就能引起解 x 较大的改变，数值稳定性差。如果 A 的条件数小， b 有微小的改变， x 的改变也很微小，数值稳定性好。它也可以表示 b 不变，而 A 有微小改变时， x 的变化情况。矩阵的条件数总是大于 1。正交矩阵的条件数等于 1，奇异矩阵的条件数为无穷大，而病态矩阵的条件数则为比较大的数据。

P.S. 这周就到这儿吧。已经很多内容了。

参考文献

  1. J H Ferziger, M Peric. Computational Methods for Fluid Dynamics. 3rd rev. ed. Berlin: Springer-Verlag, 2002
  2. Jonathan Richard Shewchuk. An Introduction to the Conjugate Gradient Method Without the Agonizing Pain. 1994
  3. wikipedia. 共轭梯度法
  4. D Flip Flop. 线性方程组(9)-预条件子（上）
4 个赞