当使用湍流模型时,需要注意的是网格的要求,特别是近壁面区域,因为大多数湍流模型都是在湍流充分发展的前提下推导出来的,在近壁面区域,这一条件会失效,因此,在近壁面区域,需要特别处理。
- 一种方法是使用某些可扩展至低雷诺数模型的湍流模型,这些模型的第一层网格必须在粘性层内,最好 (y+ = 1) ,因此需要大量的网格,也会消耗大量的计算资源。关注壁面上的力时,使用这种方法可得到较好的结果。
- 第二种方法是采用壁面函数,以解析近壁面的流场。壁面函数通常是经验性的,但满足近壁面的物理特性。近壁面网格的中心通常需要处于对数律区域以确保结果的准确性。壁面函数就是作为壁面与充分发展湍流区域 (outer layer) 之间的连接。当采用壁面函数时,不必求解边界层,因此可减少网格并节约大量的计算资源。
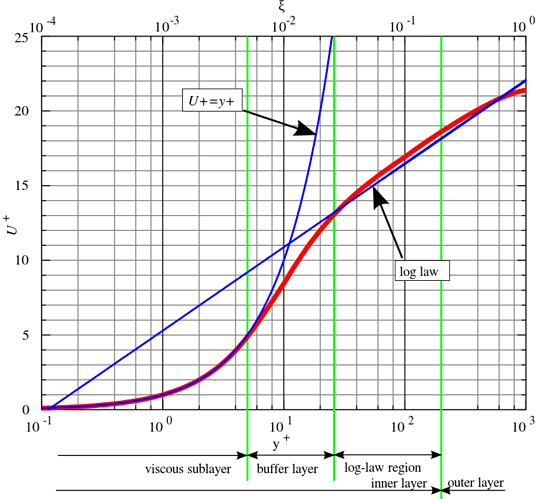
下图为近壁面区域的速度分布,
图中,
以上各式中, u^+ 为无量纲速度, y^+ 为无量纲距壁面的距离, u_t 为摩擦速度, \tau_\text{wall} 为壁面的剪应力。
在 y^+<5 的粘性区域内,
在 5<y^+<30 的区域内
在 30<y^+<200 内,
式中, \kappa 为冯卡门常数 ( Von Kármán constant),通常认为 \kappa \approx 0.41 。
使用湍流模型的目的就是要减少网格数,当选用 RAS 模型时,
- 高雷诺数:近壁面第一层网格应在 30<y^+<200 范围内,如 k-\varepsilon ,RNG k-\varepsilon 。(Fluent 采用 11.225<y^+<200),但各个学者推荐的范围是不一样的,一般在 30-60 之内肯定是没有问题的。也有推荐 10-110 甚至 200 的。 y^+ 的值合理,意味着你的第一层边界网格布置比较合理,如果 y^+ 不合理,就要调整你的边界层网格。有的 y^+ 甚至超过了 200。
- 低雷诺数:求解粘性层 (viscous-sublayer),通常这一区域需要约 10~20 层网格,最好 y^+=1 ,如 k-\omega 模型。
当选用 LES 模型时,
- 需要解粘性层 (viscous sublayer)
- 需要高阶格式
- 最好是各向同性的网格 (网格尽可能为等边的)
如何根据 y+ 计算第一层网格的高度
- 第一种方法,直接利用网络 https://www.cfd-online.com/Tools/yplus.php
- 第二种方法
- 根据雷诺数计算摩擦系数 C_f = 0.0576 Re^{-\frac{1}{5}} ,摩擦系数的估计有不同的公式,请参考 https://www.cfd-online.com/Wiki/Skin_friction_coefficient
- 根据摩擦系数计算壁面剪应力 \tau_\text{wall} = \dfrac{1}{2} C_f \rho U^2_\infty
- 计算摩擦速度 u_t = \sqrt{\dfrac{\tau_\text{wall}}{\rho}}
- 计算第一层网格高度 y=\dfrac{y^+ \nu}{u_t} (\nu 为运动粘度)
你所关注的流动是不是湍流?
雷诺数
外流
内流
自然对流
壁面函数如何设置
壁面函数在 nut 中设置,如:
wallPatch
{
type nutkWallFunction;
value 1e-7;
}
主要类型有
-
nutWallFunction(最基础的壁面函数): 基于 k 的高雷诺数模型,在 OpenFOAM-ext 版本中,仍然保留了这一类型,而在 OpenFOAM-4.x 后续的版本中,这一类型仅作为基类,提供虚函数 -
nutkWallFunction(k-\omega 模型): 基于对数律设置第一层网格节点的紊流粘度(turbulent viscosity) -
nutUWallFunction:基于壁面附近的速度计算 y^+ -
nutUSpaldingWallFunction(SA模型标配,早期版本中叫 nutSpalartAllmarasWallFunction):覆盖 y^+ 从 O(1) 到 O(10) 的连续壁面函数,当 y^+ 变化范围较大时优先选择 -
nutLowReWallFunction(代码注释: “Sets nut to zero, and provides an access function to calculate y+.” ):在模拟中计算yPlusRAS所需的虚壁面函数,用于求解近壁流动(有争论)
k,\,\epsilon,\,\omega 的设置:
-
epsilon:epsilonWallFunction,lowRe计算中设为固定值 \epsilon=0 或 \epsilon=10^{-8} 。对于每个时间步,通过使用从经典对数定律公式来计算第一个网格点值。 -
k|q|R:kqRWallFunction,貌似在 y^+\approx 1 依然有效,但对于 y^+<1 应采用固定值 k=0 或一个足够小的值 -
omega:omegaWallFunction,边界条件而非真正的壁面函数,对于 k-\omega 模型,不论 y^+ 为多少均应该采用。 \omega_\text{wall}=\dfrac{60\nu}{\beta y^2},\,\,\beta=0.075 - 在壁面函数中赋值的
value仅作为 初始值。
位于 src/TurbulenceModels/turbulenceModels/derivedFvPatchFields/wallFunctions/nutWallFunctions/nutWallFunction 文件夹的 nutWallFunctionFvPatchScalarField.C 内容里
void Foam::nutWallFunctionFvPatchScalarField::updateCoeffs()
{
if (updated())
{
return;
}
operator==(calcNut());
fixedValueFvPatchScalarField::updateCoeffs();
}
上一段程序中操作符 == 定义为 calcNut() ,指的是计算将会在 calcNut() 中进行,湍流粘度则在每一个边界的面上生成。函数 calcNut() 被定义为虚函数,并被初始化为 0 (初始化操作在 nutWallFunctionFvPatchScalarField.H)。
//- Calculate the turbulence viscosity
virtual tmp<scalarField> calcNut() const = 0;
calcNut() 会在不同的 nutWallFunction 中重新定义。
我们先来看一下 nutLowReWallFunction,这一段程序位于 nutLowReWallFunctionFvPatchScalarField.C :
tmp<scalarField> nutLowReWallFunctionFvPatchScalarField::calcNut() const
{
return tmp<scalarField>(new scalarField(patch().size(), 0.0)); // 返回 0 的场
}
以下是 nutkWallFunction 的 calcNut() 函数重载
tmp<scalarField> nutkWallFunctionFvPatchScalarField::calcNut() const
{
const label patchi = patch().index(); // 获取边界的标签
const turbulenceModel& turbModel = db().lookupObject<turbulenceModel>
( // 查找湍流模型并将地址传给 turbModel
IOobject::groupName
(
turbulenceModel::propertiesName,
internalField().group()
)
);
const scalarField& y = turbModel.y()[patchi];
const tmp<volScalarField> tk = turbModel.k();
const volScalarField& k = tk();
const tmp<scalarField> tnuw = turbModel.nu(patchi);
const scalarField& nuw = tnuw();
const scalar Cmu25 = pow025(Cmu_);
tmp<scalarField> tnutw(new scalarField(patch().size(), 0.0));
scalarField& nutw = tnutw.ref();
forAll(nutw, facei)
{
label celli = patch().faceCells()[facei];
scalar yPlus = Cmu25*y[facei]*sqrt(k[celli])/nuw[facei];
if (yPlus > yPlusLam_)
{
nutw[facei] = nuw[facei]*(yPlus*kappa_/log(E_*yPlus) - 1.0);
}
}
return tnutw;
}
参考文献
[1] https://openfoam.com/documentation/cpp-guide/html/guide-turbulence.html
[2] https://en.wikipedia.org/wiki/Law_of_the_wall
[3] https://en.wikipedia.org/wiki/Von_Kármán_constant
[4] https://www.simscale.com/forum/t/what-is-y-yplus/82394
[5] http://imechanica.org/files/fluent_13.0_lecture06-turbulence.pdf
[6] https://www.cfd-online.com/Forums/openfoam-solving/170101-wall-function-usage.html