在 icoFoam.C 中,有这么一段
pEqn.solve();
if (nonOrth == nNonOrthCorr)
{
phi -= pEqn.flux();
}
对不可压缩流体连续性方程进行离散,
\nabla\cdot U = \sum_f U\cdot S_f = \sum \phi_f
式中, \phi_f 为面通量。
将此式代入
\begin{equation}
\mathbf U_\mathrm{P}^{n+1} = \mathbf{U}^{*,n+1} - \frac{1}{A_\mathrm{P}}\nabla p^{n+1}
\end{equation}
\tag{5}
此式来自 Code of the Week #4: solve(UEqn == -fvc::grad( p))。有
\phi_f = \mathbf S_f\cdot U^{*,n+1} - \frac{1}{A_p} \mathbf S_f \cdot \nabla p
上式中的 \dfrac{1}{A_p} S_f \cdot \nabla p 出现在了压力泊松方程的离散过程中 (Code of the Week #4: solve(UEqn == -fvc::grad( p)) 式 (9) ),有
\frac{1}{A_p} \mathbf S_f \cdot \nabla p = \frac{1}{A_p} \frac{\mathbf S_f}{|\mathbf d|}( p_N - p_P) = a_N^P(p_N - p_P)
式中, \mathbf d 为相邻网格中心点距离。因为, \mathbf S = \mathbf\Delta +\mathbf k ,
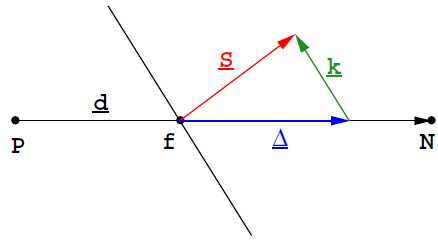
所以
\frac{1}{A_p} \mathbf S_f \cdot \nabla p = \frac{1}{A_p} \frac{\mathbf \Delta}{|\mathbf d|}( p_N - p_P) + \frac{1}{A_p} \mathbf k\cdot\nabla p
上式就是 flux() 表达式。要使通量完全守恒,必须与组成压力方程的形式一致 (使用非正交修正)。
flux() 在 fvMatrix.C 中的定义为:
template<class Type>
Foam::tmp<Foam::GeometricField<Type, Foam::fvsPatchField, Foam::surfaceMesh> >
Foam::fvMatrix<Type>::
flux() const
{
if (!psi_.mesh().schemesDict().fluxRequired(psi_.name()))
{
FatalErrorIn("fvMatrix<Type>::flux()")
<< "flux requested but " << psi_.name()
<< " not specified in the fluxRequired sub-dictionary"
" of fvSchemes."
<< abort(FatalError);
}
// construct GeometricField<Type, fvsPatchField, surfaceMesh>
tmp<GeometricField<Type, fvsPatchField, surfaceMesh> > tfieldFlux
(
new GeometricField<Type, fvsPatchField, surfaceMesh>
(
IOobject
(
"flux("+psi_.name()+')',
psi_.instance(),
psi_.mesh(),
IOobject::NO_READ,
IOobject::NO_WRITE
),
psi_.mesh(),
dimensions()
)
);
GeometricField<Type, fvsPatchField, surfaceMesh>& fieldFlux = tfieldFlux();
for (direction cmpt=0; cmpt<pTraits<Type>::nComponents; cmpt++)
{
fieldFlux.internalField().replace
(
cmpt,
lduMatrix::faceH(psi_.internalField().component(cmpt))
);
}
// This needs to go into virtual functions for all coupled patches
// in order to simplify handling of overset meshes
// HJ, 29/May/2013
forAll (psi_.boundaryField(), patchI)
{
psi_.boundaryField()[patchI].patchFlux
(
fieldFlux,
*this
);
}
if (faceFluxCorrectionPtr_)
{
fieldFlux += *faceFluxCorrectionPtr_;
}
return tfieldFlux;
}
faceH 在 lduMatrixTemplates.C 中定义
template<class Type>
Foam::tmp<Foam::Field<Type> >
Foam::lduMatrix::faceH(const Field<Type>& psi) const
{
tmp<Field<Type> > tfaceHpsi
(
new Field<Type> (lduAddr().lowerAddr().size())
);
Field<Type>& faceHpsi = tfaceHpsi();
if (lowerPtr_ || upperPtr_)
{
const scalarField& Lower = const_cast<const lduMatrix&>(*this).lower();
const scalarField& Upper = const_cast<const lduMatrix&>(*this).upper();
const unallocLabelList& l = lduAddr().lowerAddr();
const unallocLabelList& u = lduAddr().upperAddr();
for (register label face=0; face<l.size(); face++)
{
faceHpsi[face] = Upper[face]*psi[u[face]]
- Lower[face]*psi[l[face]];
}
}
else
{
// No off-diagonal. Bug fix for conjugate matrices. HJ, 27/Nov/2008
faceHpsi = pTraits<Type>::zero;
}
return tfaceHpsi;
}
Hrv 在 cfd-online.com 上提到:
If your pressure laplacian has a minus sign (-), then it’s
phi = phiHbyA + pEqn().flux()
This is the case in compressible solvers.
For incompressible solvers, the pressure laplacian has a positive sign and it’s
phi = phiHbyA - pEqn().flux()
参考文献
- Description of flux() method. Description of flux() method -- CFD Online Discussion Forums
- phi -= pEqn.flux() vs. linearInterpolate(U) & mesh.Sf() -- CFD Online Discussion Forums
- http://www.tfd.chalmers.se/~hani/kurser/OS_CFD_2010/implementApplication.pdf
- Jasak, H. Error Analysis and Estimation for the Finite Volume Method with Applications to Fluid Flows. PhD thesis. Imperial College London, 1996