我想在OpenFOAM中求解某个动量方程
方程如下:
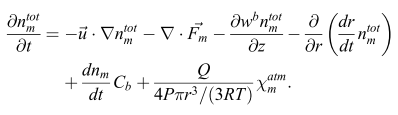
已知:
w^b 是类型为 dimentionsScalar 的已知量,
\dfrac{dr}{dt} 是类型为 dimentionsScalar 的已知量,
n^{tot} 是类型为 volScalarField 的未知量
给我带来麻烦的是等号右手边(RHS)的第三项和第四项
根据目前我掌握的知识,分析如下:
- 从形式上,这两项都可视为散度的一部分(某方向);
- 又因为这两项含有未知量 n^{tot}
- 所以,对于第三项可以表示为fvm::div(phi,wb*ntot)
问题:
- 对于第三项,按照原方程,应该是知求关于z方向的散度,但是我的表达式事实上是推求了三个方向的散度;其次是编译无法通过,提示信息为
no matching function for call to ‘div(const surfaceScalarField&, Foam::tmp<Foam::GeometricField<double, Foam::fvPatchField, Foam::volMesh> >)’
我该如何改正?我的分析是否有问题?各位如何表示方程中某一方向的散度?
- 对于第四项,形式上似乎为某个方向的散度,但其物理意义是对ntot的某一变量(r不表示方向,表示半径),这种情况下如何处理这种偏导数?
- OpenFoam中是否有基本的函数(API),用于处理定积分,偏导数?
首先说既然 n^{tot} 是待求的标量场,因此,这个方程应该不算是动量方程。如果方便的话,可以详细说明下这个方程。一般来说,关于标量 \phi 的传输方程可以做成如下的形式
\frac{\partial \phi}{\partial t} + \nabla\cdot(U \phi) = \nabla\cdot(\varGamma \nabla \phi) + S
能对应的就可以放到相应的项里面去,如果没有对应上的,就放到源项里去。
这个方程的 RHS 第三项是 \dfrac{\partial w^b n^{tot}_m}{\partial z} ,这里的 w^b 和 n^{tot} 都是标量,第四项也标量,所以第三项代表的是在 z 方向上的梯度,而不是散度。第三项本身也没有通量,而且,wb*ntot 作为临时的量也不能作为待求量,所以 fvm::div(phi,wb*ntot) 会出错。
对于某方向的偏导:
\frac{\partial \phi}{\partial z} = \vec{z}\cdot \nabla \phi
针对你的那一项
\frac{\partial w^b n^{tot}_m}{\partial z} = \vec{z}\cdot \nabla (w^b n^{tot}_m)
对于第 4 项,好像求了 r 向的偏导,但是里面又有 dr/dt ,那么最好做一个坐标转换,将其转到笛卡尔坐标系
1 个赞
感谢回复!
你说得对,我概念混淆了,这应该是一个标量输运方程;
对于我给方程的RHS第三项(以下简称为my3),我误解为成标量传输方程LHS的第二项(以下简称为you2).但实际上,由于my3中 n_{m}^{tot} 和 w_{b} 均为标量,其乘积应为标量;而散度则是作用在矢量上的,所以 my3 和 you2 并不类似. my3 表达的不是一个散度; 根据你提及的偏导数表达方法,并考虑到 w_{b} 经模化后,可以表示成一常数,my3应表达为:
wb*fvc::grad(ntot)&(0,0,1)
第四项类似处理.已经编译通过
我对您说的"做坐标变换,将其转到笛卡尔坐标系"很感兴趣,能否展开说说?r确实是半径