Code of the Week #38: div(phi, U) Gauss upwind

OpenFOAM
1

#201925

FVM 方法的积分近似需要计算控制体积表面的值，通常是因为采用了 Gauss 定理，将散度转换为了对表面的积分，然后离散：

\iiint_V\nabla\cdot(U\otimes U)=\oint_{\partial V} U\otimes U dS=\sum_f U_f \otimes \text{phi}_f

在这里，未知场是 U_f (U_f 可以是标量场，也可以代表向量场)，需要对 U_f 进行离散或插值处理。上一次 Code of the Week #36: div(phi,U) Gauss linear 讲到了 linear 的离散方法，这一次我们来讲讲 upwind 差分格式。

在使用 linear 插值格式时，容易造成解的振荡。

upwind 差分格式指定是在散度项使用，其方式为

divSchemes
{
    div(phi, U)    Gauss upwind;
}

设 U_f 为标量场。 upwind 所表示的在面 e 上插值格式为

U_{fe}= \left\{ \begin{array}% U_P, & \quad \text{if}\quad (U\cdot n)_e > 0 \\ U_E , & \quad \text{if}\quad (U\cdot n)_e < 0 \end{array} \right.

意思就是，当在 e 面上的通量为正 (向外) 时，e 上的 U 值取 U_P ，反之，取 $U_E$。

在 OpenFOAM 中，其类的继承关系是
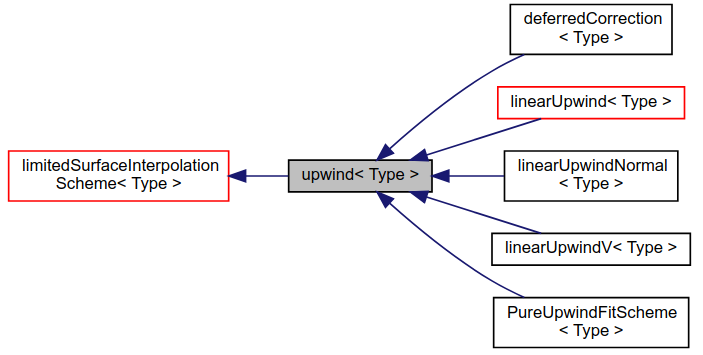
upwind-inherit
(https://www.openfoam.com/documentation/guides/latest/api/classFoam_1_1upwind.html)

upwind 继承了 limitedSurfaceInterpolationScheme，它的继承关系为
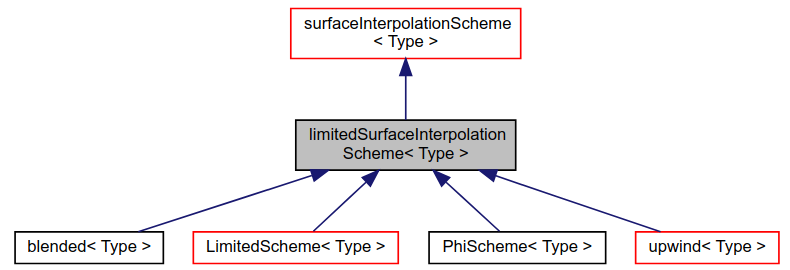
limitedSurIntScheme-inherit
(https://www.openfoam.com/documentation/guides/latest/api/classFoam_1_1limitedSurfaceInterpolationScheme.html)

limitedSurfaceInterpolationScheme 继承了 surfaceInterpolationScheme。

upwind 有三个构造函数，取其中一个：

        //- Return the interpolation weighting factors
        tmp<surfaceScalarField> weights() const
        {
            return pos(this->faceFlux_);
        }

上面一段代码的意思是

\text{weight()[facei]} = \left\{ \begin{array}% 1,&\text{if} \quad U_f > 0\\ 0,&\text{if} \quad U_f < 0 \end{array} \right.

注意，返回数据的类型是 surfaceScalarField.

根据继承关系，由于 upwind 并没有特别指明 corrected ，所以它还是继承了 surfaceInterpolateScheme.H 所设定的值：

        //- Return true if this scheme uses an explicit correction
        virtual bool corrected() const
        {
            return false;
        }

在 surfaceInterpolateScheme.C 中，

//- Return the face-interpolate of the given cell field
//  with explicit correction
template<class Type>
tmp<GeometricField<Type, fvsPatchField, surfaceMesh> >
surfaceInterpolationScheme<Type>::interpolate
(
    const GeometricField<Type, fvPatchField, volMesh>& vf
) const
{
    if (surfaceInterpolation::debug)
    {
        Info<< "surfaceInterpolationScheme<Type>::interpolate"
               "(const GeometricField<Type, fvPatchField, volMesh>&) : "
            << "interpolating volTypeField from cells to faces"
            << endl;
    }

    tmp<GeometricField<Type, fvsPatchField, surfaceMesh> > tsf
        = interpolate(vf, weights(vf));          // 根据 weights(vf) 来插值

    if (corrected())
    {
        tsf() += correction(vf);
    }

    return tsf;
}

//- Return the face-interpolate of the given cell field
//  with the given weigting factors
template<class Type>
tmp<GeometricField<Type, fvsPatchField, surfaceMesh> >
surfaceInterpolationScheme<Type>::interpolate
(
    const GeometricField<Type, fvPatchField, volMesh>& vf,
    const tmp<surfaceScalarField>& tlambdas
)
{
    ...

    const surfaceScalarField& lambdas = tlambdas();

    const Field<Type>& vfi = vf.internalField();
    const scalarField& lambda = lambdas.internalField();

    const fvMesh& mesh = vf.mesh();
    const unallocLabelList& P = mesh.owner();
    const unallocLabelList& N = mesh.neighbour();

    tmp<GeometricField<Type, fvsPatchField, surfaceMesh> > tsf
    (
        new GeometricField<Type, fvsPatchField, surfaceMesh>
        (
            IOobject
            (
                "interpolate("+vf.name()+')',
                vf.instance(),
                vf.db()
            ),
            mesh,
            vf.dimensions()
        )
    );
    GeometricField<Type, fvsPatchField, surfaceMesh>& sf = tsf();

    Field<Type>& sfi = sf.internalField();

    for (register label fi=0; fi<P.size(); fi++)
    {
        sfi[fi] = lambda[fi]*(vfi[P[fi]] - vfi[N[fi]]) + vfi[N[fi]]; // surface-interpolation caculate
    }

    // Interpolate across coupled patches using given lambdas
    // Code moved under virtual functions into fvPatchField
    // HJ, 13/Jun/2013
    forAll (vf.boundaryField(), patchI)
    {
        vf.boundaryField()[patchI].patchInterpolate
        (
            sf,
            lambdas.boundaryField()[patchI]
        );
    }

    tlambdas.clear();

    return tsf;
}

因此，当 U_f > 0 时，

\begin{align} \text{sfi[fi]} & = \text{lambda[fi]} \times \left\{\text{vfi[P[fi]] - vfi[N[fi]]}\right\} + \text{vfi[N[fi]]}\\ & = \text{weight()[fi]}\times\left\{\text{vfi[P[fi]] - vfi[N[fi]]}\right\} + \text{vfi[N[fi]]}\\ & = 1\times\left\{\text{vfi[P[fi]] - vfi[N[fi]]}\right\} + \text{vfi[N[fi]]}\\ & = \text{vfi[P[fi]]} \end{align}

因此，当 U_f < 0 时，

\begin{align} \text{sfi[fi]} & = \text{lambda[fi]} \times \left\{\text{vfi[P[fi]] - vfi[N[fi]]}\right\} + \text{vfi[N[fi]]}\\ & = \text{weight()[fi]}\times\left\{\text{vfi[P[fi]] - vfi[N[fi]]}\right\} + \text{vfi[N[fi]]}\\ & = 0\times\left\{\text{vfi[P[fi]] - vfi[N[fi]]}\right\} + \text{vfi[N[fi]]}\\ & = \text{vfi[N[fi]]} \end{align}
1 个赞