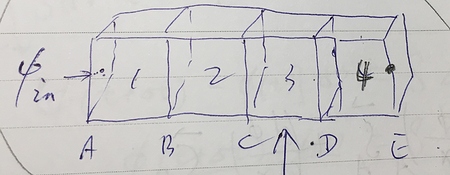
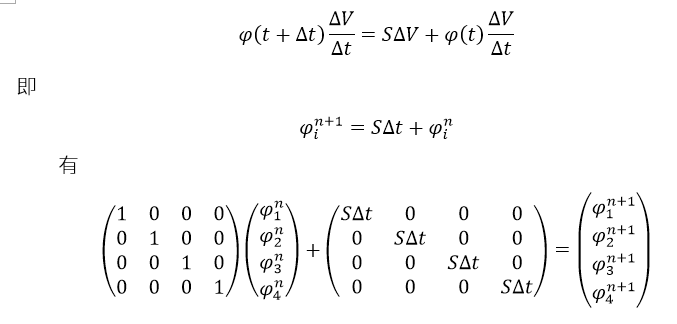本周,我们讨论一下这一个语句:
fvm::ddt(U);
这一项是动量方程
\frac{\partial U}{\partial t} + \nabla\cdot(UU) = -\nabla p + \nabla\cdot\tau
的左边第一项。
求解这一方程时,需要对 p 和 U 进行解耦。但是,本周,我们不讨论解耦的问题,而讨论一下时间项是如何离散的。为方便说明,设
\frac{\partial U}{\partial t} = S
右边的 S 为源项。
大家都知道,FVM 方法是建立在离散的空间网格上的,对这一项进行离散(积分)的方法就是
\iiint_V\int_t^{t+\Delta t} \frac{dU}{dt} = [\varphi(t+\Delta t) -\varphi(t)] \Delta V = S\Delta V \Delta t
变换一下,
[\varphi(t+\Delta t) -\varphi(t)] \frac{\Delta V}{\Delta t} = S\Delta V
则在新的时间步
\varphi(t+\Delta t)\frac{\Delta V}{\Delta t} = S\Delta V + \varphi(t)\frac{\Delta V}{\Delta t}
若 S=0 ,则有
\varphi(t+\Delta t)\frac{\Delta V}{\Delta t} = \varphi(t)\frac{\Delta V}{\Delta t}
下面,以 \varphi^{n+1} 代替 \varphi(t+\Delta t) , 以 \varphi^{n} 代替 \varphi(t) 。
如果以一均分网格作为示例,
有
\left[
\begin{array}%
\frac{V}{\Delta t} & 0 & 0 & 0\\
0 & \frac{V}{\Delta t} & 0 & 0 \\
0 & 0 & \frac{V}{\Delta t} & 0\\
0 & 0 & 0 & \frac{V}{\Delta t}
\end{array}
\right]
\times
\left[
\begin{array}%
\varphi_1^{n+1}\\
\varphi_2^{n+1}\\
\varphi_3^{n+1}\\
\varphi_4^{n+1}\\
\end{array}
\right]
=
\left[
\begin{array}%
\varphi_1^n\frac{V}{\Delta t}\\
\varphi_2^n\frac{V}{\Delta t}\\
\varphi_3^n\frac{V}{\Delta t}\\
\varphi_4^n\frac{V}{\Delta t}\\
\end{array}
\right]
获得这一矩阵后,再与动量方程的其他项离散后得到的矩阵相加,如上一期的 Code of the Week #1: div(phi,U) ,就可以形成动量方程离散后的完整矩阵方程。
以下程序段为 foam-extend-3.1 内, 源文件 src/finiteVolume/finiteVolume/ddtSchemes/EulerDdtScheme/EulerDdtScheme.C
从第 260 行起:
template<class Type> // 类模板
tmp<fvMatrix<Type> > // 返回类型: fvMatrix 矩阵
EulerDdtScheme<Type>::fvmDdt // 类名::函数名,定义
( // 对 vf 进行时间项离散
GeometricField<Type, fvPatchField, volMesh>& vf // vf 是参数
)
{
tmp<fvMatrix<Type> > tfvm // 矩阵定义及初始化,返回的变量
(
new fvMatrix<Type>
(
vf,
vf.dimensions()*dimVol/dimTime
)
);
fvMatrix<Type>& fvm = tfvm();
scalar rDeltaT = 1.0/mesh().time().deltaT().value(); // 1/deltaT
fvm.diag() = rDeltaT*mesh().V(); // 对角线 V/deltaT
if (mesh().moving()) // 网格是否有移动
{
fvm.source() = rDeltaT*vf.oldTime().internalField()*mesh().V0();
}
else
{
fvm.source() = rDeltaT*vf.oldTime().internalField()*mesh().V(); // RHS,vf*V/deltaT
}
return tfvm;
}
在程序中,返回的矩阵里面 0 元素位置上是空的,以节约内存。也就是说,返回的值中,包括矩阵对角线上的值,和等式右边的值 (源项)。 S 在 ddt() 中没有体现,将另外说明。