在 system/fvSchemes 里，经常见到
laplacianSchemes
{
laplacian(rAU, p) Gauss linear corrected;
}
laplacianSchemes 是在 system/fvSchemes 文件里的子字典，指定 laplacian 项的离散格式，其语法是
laplacianSchemes
{
default none;
laplacian(gamma,phi) Gauss <interpolationScheme> <snGradScheme>;
}
其代表的意义是
\nabla\cdot(\Gamma\nabla \phi) = \Gamma\nabla^2 \phi = \Gamma\left(\frac{\partial^2}{\partial x_1^2} \phi + \frac{\partial^2}{\partial x_2^2} \phi + \frac{\partial^2}{\partial x_3^2} \phi\right)
FVM 方法
\nabla\cdot \left( \Gamma \nabla \phi \right) = \frac{1}{V}\int_V \nabla\cdot \left( \Gamma \nabla \phi \right)dV = \frac{1}{V} \oint_S \Gamma \nabla \phi d\vec{S} = \frac{1}{V} \sum_i^{\mathrm{nFace}}\left(\nabla{\phi}\right)_{f,i} \cdot \Gamma_f \vec{S}_{f,i}
Laplacian 項离散为该控制体所有面的面法向量与該面上 \phi 的梯度的点积之和。从体心到面心需要一种插值方法 (interpolationScheme) 。
面法向梯度 (Surface-normal Gradient) 指的是在 f 面上的法向梯度，面上的 \phi 的梯度可由 基于控制体的梯度插值求得。
\nabla_f^\perp \phi = \vec{n} \cdot \left( \nabla \phi \right)_f
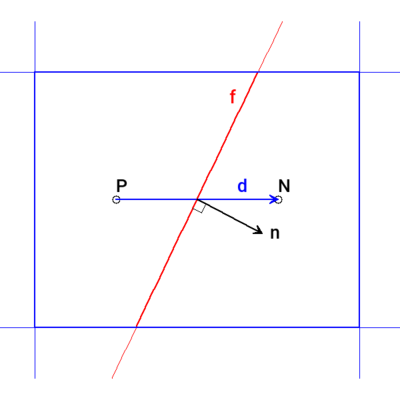
d 和 n 向量间的夹角代表了非正交性。
工程分析中的网格划分并不总是正交网格。因此，为保证二阶精度，用隐式正交量加上显式非正交修正的方式，即 corrected 格式，
\nabla_f^\perp \phi = \underbrace{\alpha \frac{\phi_P - \phi_N}{| \vec{d} |}}_{\mathrm{implicit}} + \underbrace{\left( \hat{\vec{n}} - \alpha \hat{\vec{d}} \right) \cdot \left( \nabla \phi \right)_f}_{\mathrm{explicit\ correction}}
式中， \alpha = \frac{1}{\cos(\theta)}
当非正交角 \alpha 增加时，修正量也增加。当 \alpha \rightarrow 90^\circ ，显式修正量可能会很大以致方程的解不稳定。这时，可以在其格式前面增加 limited 字段，但还需要系数 \psi \in [0,\,1] ，
\psi = \begin{cases}
\begin{array}{ll}%
0 & \text{不修正，相当于 uncorrected}\\
0.333 & \text{非正交修正} \leqslant 0.5\times 正交量\\
0.5 & \text{非正交修正} \leqslant 正交量\\
1 & \text{非正交修正,相当于 corrected}
\end{array}
\end{cases}
一般情况下， \psi 取 0.33 或 0.5，0.33 提供较好的稳定性，0.5 提供较高的精度。如果 \nabla\cdot(\Gamma\nabla \phi) 需要考虑非正交修正，其离散格式可按以下指定：
laplacianSchemes
{
//default Gauss linear uncorrected;
laplacian(gamma,phi) Gauss linear limited corrected 0.33;
}
在旧的版本中 (如 ext-3.1)，设置为
laplacianSchemes
{
//default Gauss linear uncorrected;
laplacian(gamma,phi) Gauss linear limited 0.33;
}
参考